| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- Floating
- Big size image
- pullup
- #9
- Softmax
- autoencoder
- Circuit
- assignment1
- 풀업저항
- KNN
- neural net
- Solution
- atmega128
- impl
- error
- 회로
- 풀다운저항
- pulldown
- cs231n
- two-layer neural net
- assignment
- Features
- palindrome
- leetcode
- TensorFlow
- pyTorch
- Backpropagation
- backward pass
- NotFoundError
- softmax backpropagation
- Today
- Total
코딩공부
Backpropagation, Intuitions 본문
지난글에 언급했듯이 Backpropagation, Intuitions 부분을 번역해보았다.
Slide가 아닌 http://cs231n.github.io/optimization-2/ 에 있는 내용으로 Slide기준 Lecture 4에 포함된 내용이다.
Slide의 일부도 필요에따라 끌어와 사용하였다.
Introduction
Motivation. In this section we will develop expertise with an intuitive understanding of backpropagation, which is a way of computing gradients of expressions through recursive application of chain rule.(of가 참 많다) Understanding of this process and its subtleties is critical for you to understand, and effectively develop, design and debug Neural Networks.
Motivation. 이번 섹션에서 우리는 chain rule의 반복적인 사용을 통해 gradients를 계산하는 방법인, backpropagation의 직관적인 이해를 통해 전문지식을 발전시킬것이다. 이러한 과정과 세부 요소들을 이해하는것은 Neural Networks를 효과적으로 발전시키고, 설계하고, 디버그하는데 매우 중요하다.

Problem statement. 이번 섹션에서 공부할 중요한 문제는 다음과 같다. : 우리는 x가 inputs의 vector인 함수 f(x)를 가지고 x에서의 f의 gradient를 계산할 것이다.

Motivation. Neural Networks중 f는 loss function ( L )과 관련이 있고 inputs x는 training data와 neural network weights로 이루어져 있는 경우에 이 문제에 관심이 있는 가장 큰 이유를 떠올려보자. 예를들어, loss는 SVM loss function이고 input들은 training data와 weights, biases이다. training data가 주어져 고정되어있고, weights를 우리가 제어할 변수라고 생각하자(Machine Learning의 일반적인 경우들처럼). 그러면, 우리는 input examples xi에 대해 gradient를 구하는데 backpropagation을 용이하게 쓸 수 있지만, 실제로는 W나 b같은 parameters에 대한 gradient를 구하는데에만 사용하기 때문에 우리는 이것을 parameter update에 사용한다.(xi에 대해서도 gradient를 구할수 있긴 하지만 xi는 이미지이고, fixed, given 값이기 때문에 W,b의 gradient를 구해서 update하는데 backpropagation을 한다는 의미라고 생각한다.) 그러나 나중에 이야기하겠지만 xi에 대한 gradient도 가끔 유용하다. 예를들어 visualization의 목적과 Neural Network가 무엇을 하는지를 알려주는데 사용될 수 있다.
이 강의를 들으면 chain rule을 이용하여 gradient를 유도하는것이 편해질것이고, 우리는 최소한 여러분이 이 section을 훑어보기라도 했으면 한다, 이 section은 매우 적게 발전된 측면인 실수치의 circuit들에서의 backward flow로써의 backpropagation을 보여주기 때문에 여러분이 얻을 시야는 전체 수업에 도움이 될것이다.


Simple expressions and interpretation of the gradient
복잡한 표현에서 표기법과 관습적인 패턴을 발전시키기 위해 간단한것부터 시작해보자. 두수의 곱으로 이루어진 간단한 곱 함수를 생각해보자. 각각의 input에 대해 편미분식을 유도하는것은 쉽다.
Interpretation. 미분식들이 무엇을 말하는지 염두해두자: 미분식들은 특정 위치에서 매우 작은 범위에서의 변수에 대한 함수의 변화비를 의미한다.
좌변의 나눗셈 기호의 기술적 의미는, 우변의 기호와 다르게, 나눈다는 의미가 아니다. 대신, 이 표기법은 연산자 d/dx가 함수 f에 적용되고 미분식을 반환한다는 것을 의미한다. 위의 표현식을 이해하는 좋은 방법은 h가 매우 작을때, 함수는 직선에 잘 근사하고, 미분식은 함수의 기울기이다. 다시말해, 각각의 변수에 대한 미분식은 여러분에게 각 변수에서 전체 함수의 감도(기울기)를 알려준다. 예를들어, x =4, y = -3이면 f(x,y) = -12 이고, x에대한 미분식 df/dx = -3이다. 이것이 의미하는 것은 우리가 x를 아주작은 양만큼 증가시키면, 함수값은 증가량의 3배만큼 줄어들것이다(-부호때문에). 이것은 위에 있는 식을 재배열하면 이해할 수 있다. 비슷하게, df/dy = 4이기 때문에, 우리는 y를 매우 작은값 h만큼 증가시키면, output이 4h만큼 증가할 것을 예상할 수 있다(+부호때문에).
각각의 변수에대한 미분식은 각 변수에 대한 전체 표현식(함수)의 감도(기울기)를 의미한다.
위에서 언급했듯이, gradient ∇f는 편미분의 벡터이고, 그러므로 우리는 ∇f = [df/dx, df/dy] = [y,x] 라고 둘 수 있다. gradient가 엄밀히 따지면 vector이긴 하지만, 우리는 간단히 "x에 대한 편미분값"이라는 표현 대신 "x에 대한 gradient"같은 표현법을 사용한다.
우리는 또한 덧셈 연산자에 대해서도 미분식들을 구할 수 있다.
f(x,y) = x + y -> df/dx = 1, df/dy = 1
즉, x, y에 대한 미분식은 둘 다 x, y값에 관계가 없다. 이것은 x, y의 증가가 f의 output도 증가시키고, x, y의 값에 독립적이기 때문에 당연한것이다(위에서 보여준 곱하기 함수와는 다르게). 마지막으로 우리는 max 연산자에 대해 알아보자.
f(x,y) = max(x,y) -> df/dx = 1(x>=y) df/dy = 1(y>=x)
즉, 더 큰 input의 gradient는 1이고 작은쪽은 0이다. 직감적으로, 만일 input들이 x = 4, y = 2면, max는 4이고, 함수값은 y의 변화와는 관계가 없다. 즉, 만일 우리가 y를 매우 작은 h만큼 증가시켜도, 함수는 여전히 4를 출력할 것이고, 그러므로 gradient는 0이 될것이다: y의 증가는 아무 의미(효과)가 없다. 물론, 만일 우리가 y를 크게 바꾼다면(예를들어 2보다 큰 값만큼), f의 결과값은 바뀌겠지만, 미분식은 함수의 input에 그런 큰 변화를 주는것이 아니다. 미분식들은 lim h->0 로 표현될수 있을정도로 input이 매우 조금 변할때 의미가 있다고 정의되어 있다.

Compound expressions with chain rule
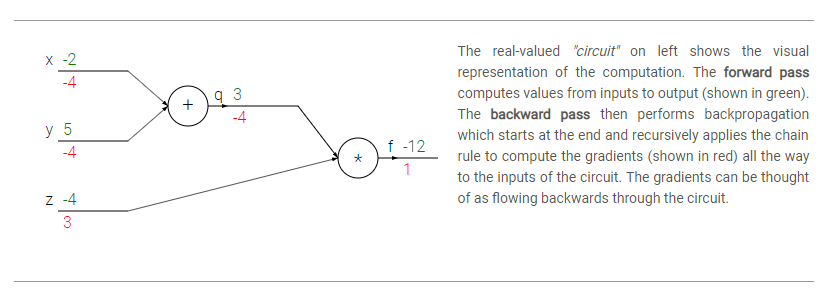
f(x,y,z) = (x+y)z 같은 여러개의 함수로 이루어진 복잡하게 표현된 식들을 생각해보자. 이 식은 여전히 직접 미분하기에 충분히 간단하지만, 우리는 backpropagation의 직관적인 이해에 도움이 될수 있도록 특별한 접근법을 사용할 것이다. 특히, 이 식은 두개의 식으로 나눠질수 있다는것을 알아두자: q = x+y 와 f = qz. 게다가 우리는 두 식을 어떻게 미분하는지 이전 section에서 배웠다. f는 q와 z의 곱이므로, df/dq = z, df/dz = q이고 q는 x와 y의 합이므로 dq/dx = 1, dq/dy = 1이다. 그러나 df/dq값은 쓸모가 없기때문에 필수적으로 신경쓸필요는 없다. 대신, 우리는 궁극적으로 inputs x,y,z에 대한 f의 기울기에 관심이 있다. chain rule은 이 기울기 값들(df/dz, dq/dx, dq/dy 등등)을 곱셈연산을 통해 chain하는 올바른 방법을 알려준다. 예를들어, df/dx = df/dq * dq/dx와 같이. 실제로 이것은 두개의 기울기를 의미하는 간단한 두개의 수의 곱이다. 예시를 보자.
결과적으로 우리는 x,y,z에대한 f의 감도(기울기)인 [dfdx, dfdy, dfdz]값들을 알게된다. 이것이 backpropagation의 가장 간단한 방법이다. 더 나아가서, 우리는 df부분을 계속 적지 않아도 되는 간단한 표기법을 원한다. 즉, 예를들어 dfdq대신 간단히 dq라고 작성하고, 항상 마지막 결과값에 대한 기울기라고 가정한다.
계산은 circuit diagram을 통해 시각화하기 좋다.
---------뒤는 전체를 번역하는것이 효율면에서 너무 좋지 않다고 생각되어 중요한 부분들만 요약하여 작성하겠다.-------
'ML , DL (2019) > cs231n' 카테고리의 다른 글
| cs231n assignment1 - two-layer neural net (0) | 2020.01.10 |
|---|---|
| backpropagation, intuition - 2 (요약) (0) | 2019.09.01 |
| assignment1 - softmax (0) | 2019.08.20 |
| cs231n assignment1 - SVM (0) | 2019.08.17 |
| cs231n assignment1 - knn (6) | 2019.08.14 |