| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- pullup
- Features
- Solution
- two-layer neural net
- Backpropagation
- 풀업저항
- #9
- 풀다운저항
- Floating
- error
- palindrome
- Big size image
- TensorFlow
- assignment
- cs231n
- atmega128
- KNN
- autoencoder
- pulldown
- Circuit
- assignment1
- backward pass
- impl
- NotFoundError
- 회로
- Softmax
- pyTorch
- leetcode
- softmax backpropagation
- neural net
- Today
- Total
코딩공부
cs231n assignment1 - SVM 본문
강의 내용 중 SVM에 관한 설명 부분을 번역해 보았습니다.
There are several ways to define the details of the loss function. As a first example we will first develop a commonly used loss called the Multiclass Support Vector Machine (SVM) loss. The SVM loss is set up so that the SVM “wants” the correct class for each image to a have a score higher than the incorrect classes by some fixed margin Δ. Notice that it’s sometimes helpful to anthropomorphise the loss functions as we did above: The SVM “wants” a certain outcome in the sense that the outcome would yield a lower loss (which is good).
loss function의 details를 정의하는 방법에는 몇 가지가 있다. 첫 번째로 많이 사용되는 SVM, Multiclass Suport Vector Machine Loss를 다룬다. SVM loss는 단지 설정(set up)이므로 각 이미지는 incorrect class보다 fixed margin Δ만큼 더 큰 score를 갖는 correct class를 '원한다'(필요로 한다). 위에서 얘기했듯 loss function을 의인화하는 것은 때때로 도움이 된다는 것을 알아두자. SVM은 lower loss(좋은)를 만들어 주는 결과를 원한다.(직역 - SVM은 명확한 결과 , 낮은 loss를 내는 결과라는 의미에서, 를 원한다)
마찬가지로 전체 코드, .py, .ipynb 파일들은 github.com/Lee-daeho/cs231n 에서 확인할 수 있다.
SVM부터는 코드를 보여주고 어떤 의미인지 설명하는 방식으로 글을 작성하겠다.
assignment1 - SVM

해당 함수에서 우리가 작성해야 할 부분은 loss function의 gradient인 dW를 구하는 것이다.
이를 구하기 위해 loss function부터 다시 알아보자.
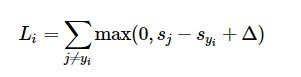
위의 Li가 i번째 이미지의 loss function이다. 0과 sj - syi + Δ 중 큰 것들의 합인데 이때 yi는 위에서 이야기한 correct class이고 해당 class의 score이다. score는 Wx의 형태로 나타나는데, 10개의 class가 있고 이미지는 5개의 32 x 32 x 3이라고 하면 x는 5 x 3072, W는 3072 x 10의 크기를 갖는 행렬이 되고 둘의 내적(곱)인 score는 5 x 10의 크기를 갖는 행렬이 될 것이다. n x m이라 하면(n = 5, m = 10), n번째 이미지의 m번째 클래스에 대한 score의 행렬이라고 할 수 있겠다. 즉 위 식에서 sj와 syi는 sj는 각각 score[i,j], score[i,yi]를 의미한다.
자 이제 gradient를 구하는 방법에 대해 알아보자. 이 방법은 cs231n lecture note에 설명되어 있으므로 이를 이용하겠다.

맨 위의 식은 한 개의 datapoint에 대한 SVM loss function이다.
우리는 위의 식을 weights에 대해 미분을 할 수 있다. 예를 들어 wyi에 대해 편미분을 해주면 위의 두 번째 식을 얻을 수 있다.
1은 괄호 안의 식이 참인지 0인지 알려주기 위한 지표(indicator function)이다. 표현이 괴랄하게 보일 수 있지만, 이 코드를 이용하면 desired margin(delta)를 만족하지 않는(반대로 loss function에 영향을 주는) class의 개수를 쉽게 셀 수 있고, data vector xi는 gradient의 갯수에 따라 행렬의 크기가 변경된다. 이 gradient는 correct class와 관련있는 W의 행에 대한것임을 알아둬라. j =/= yi인 행에서 gradient는 맨 아래식과 같이 표현된다.
이 식들을 유도해냈다면 그대로 적용하여 gradient를 update하는데 사용하면 된다.
다음은 svm_loss와 dW를 위의 방식이 아닌 vectorize하여 구하는 방법이다.

위의 방법을 따라가되 for문같은 반복문을 쓰지 않고 행렬전체를 이용하여 loss와 dW를 구한다.
scores는 X와 W의 내적(행렬 곱)이고, 그중 correct_class의 score들은 i,yi번째이므로 range함수와 y를 이용하여 찾을 수 있다.
이후 fixed margin(delta)를 loss_naive때와 같이 1로 두고 scores행렬의 모든 원소에 더하기 위해 scores와 같은크기의 ones 행렬을 만든다. 이때 correct_class에는 적용되면 안되므로 delta 행렬의 해당 위치의 원소 값을 0으로 만든다.
이후 loss를 구하기 위해 margin을 먼저 구하는데 이 margin과 fixed margin(delta)와는 다른것이므로 구분이 필요하다. margin을 보두 구한 뒤 각 행을 모두 더해 loss를 구하고 regularization을 해주면 된다. dW를 구하는 부분도 위에서 했던 loss_naive 함수를 참고하면 간단하게 작성할 수 있다.
다음은 learning_rate와 regularization_strength, 최적의 hyper-parameter를 구하기 위해 validation을 하는 과정이다.
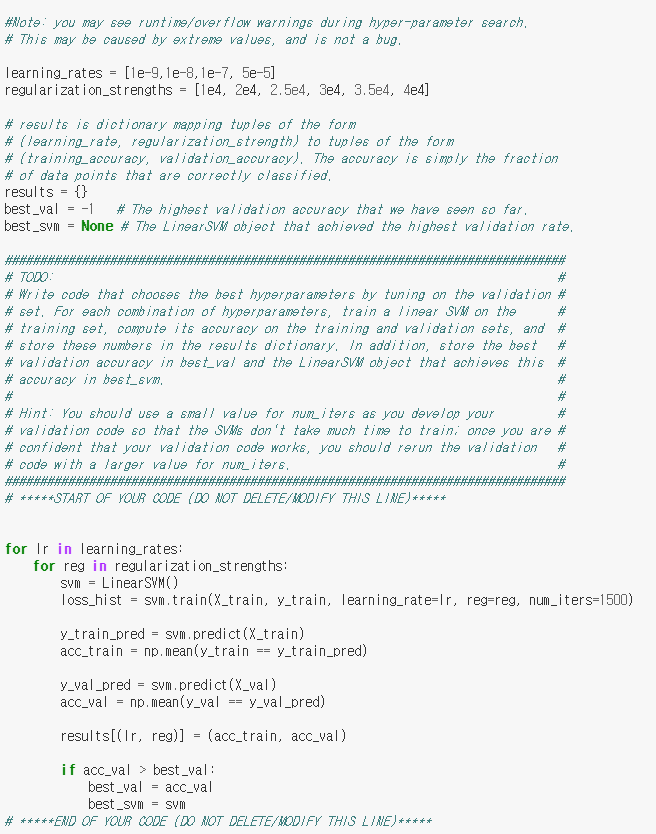
learning_rates와 regularization_strengths는 원래 2개씩 값이 들어가 있으나 더 많은 경우에 대해 실험을 해볼 수 있다. 사진에 보이는 것 외에 다른 경우들도 실험해 보았으나 learning_rate의 경우 1e-7, regularization strength의 경우 1e4가 accuracy값이 가장 괜찮게 나왔다. 기본값으로 정해져 있던것으로 기억하니 굳이 다른 값을 추가하지 않아도 될 것 같다.
이후 learning_rates와 regularization_strengths에 대해 각각 train을 진행한 뒤 결과를 확인하여 최적의 값을 가진 svm을 best_svm에 저장한다. 이후 이 best_svm을 이용하여 learned weights를 visualization하는데 이 결과는 다음과 같았다.

다음은 softmax classifier입니다.
코드 및 사진 출처 - cs231n.github.io
'ML , DL (2019) > cs231n' 카테고리의 다른 글
| cs231n assignment1 - two-layer neural net (0) | 2020.01.10 |
|---|---|
| backpropagation, intuition - 2 (요약) (0) | 2019.09.01 |
| Backpropagation, Intuitions (0) | 2019.08.22 |
| assignment1 - softmax (0) | 2019.08.20 |
| cs231n assignment1 - knn (6) | 2019.08.14 |